奇函数与偶函数相乘的结果特性分析

奇函数与偶函数的概念是数学中的基础概念之一，它们在函数的性质研究中占据着重要地位。今天，我们将探讨一个有趣的问题：奇函数乘以偶函数等于什么？这个问题不仅能够帮助我们深入理解函数的基本特性，还能激发我们对数学规律的兴趣和探索。

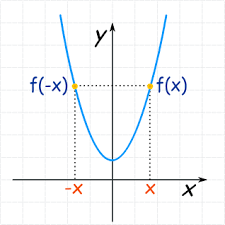
首先，让我们回顾一下奇函数和偶函数的定义。如果对于定义域内的任意x值，都有f(-x) = -f(x)，那么这个函数被称为奇函数；相反，如果对于定义域内的任意x值，都有f(-x) = f(x)，则该函数被称为偶函数。简单来说，奇函数关于原点对称，而偶函数则关于y轴对称。

接下来，我们来解答奇函数乘以偶函数等于什么？这个问题。假设f(x)是一个奇函数，g(x)是一个偶函数。根据定义，我们有：

- 对于奇函数f(x)，f(-x) = -f(x)

- 对于偶函数g(x)，g(-x) = g(x)

现在，我们考虑这两个函数相乘得到的新函数h(x) = f(x) * g(x)。为了探究h(x)的性质，我们可以计算h(-x)：

⁄⁄[ h(-x) = f(-x) * g(-x) ⁄⁄]

根据奇函数和偶函数的定义，将f(-x)替换为-f(x)，g(-x)替换为g(x)，得到：

⁄⁄[ h(-x) = (-f(x)) * g(x) ⁄⁄]

⁄⁄[ h(-x) = -(f(x) * g(x)) ⁄⁄]

⁄⁄[ h(-x) = -h(x) ⁄⁄]

从上述推导可以看出，h(x)满足奇函数的定义条件，即h(-x) = -h(x)。因此，可以得出结论：奇函数乘以偶函数的结果是一个奇函数。

这个结论不仅加深了我们对奇函数和偶函数性质的理解，也展示了数学世界中不同函数之间相互作用的美妙之处。通过这样的学习和探索，我们不仅能掌握更多的数学知识，还能培养逻辑思维能力和问题解决能力。希望本文能够激发读者对数学的兴趣，并鼓励大家在日常的学习和生活中不断探索和发现新的知识。